TIL - 20.12.10

1 minute read

Merge Sort

Quick Sort

구현
직접 구현해서는 사용하지 말 것!!!!
- 예시 → 시간초과로 통과하지 못함

주의 & 실수

base condition

수정코드

퀵 소트를 직접 구현하여 쓰지말아야하는 이유

퀵소트의 최악의 경우는 O(n^2) 이 나올 수 있다. pivot을 설정하는 방식에 따라 달라질 수 있다.

pivot을 제자리로 보내야 하는 리스트들의 길이의 합은 N이어서 각 단계마다 O(N)이 필요하다고 생각할 수 있습니다. 그러면 pivot이 매번 완벽하게 중앙에 위치해서 리스트를 균등하게 둘로 쪼갠다면 단계의 개수는 머지 소트때와 같이 lg N이 될거고 이 경우에는 퀵 소트의 시간복잡도가 O(NlgN)입니다.

물론 늘 pivot이 중앙에 위치하는 이상적인 상황이 생기지는 않겠지만 pivot이 매번 어느 정도로만 잘 자리잡는다면 시간복잡도는 여전히 O(NlgN)입니다. 예를 들어 pivot이 매번 리스트를 1대 99의 배율로 쪼개더라도 시간복잡도는 O(NlgN)이란걸 수학적으로 보일 수 있습니다. 또 앞에서 말한 cache hit rate이 높다는 점 덕분에 퀵 소트는 속도가 굉장히 빠릅니다.

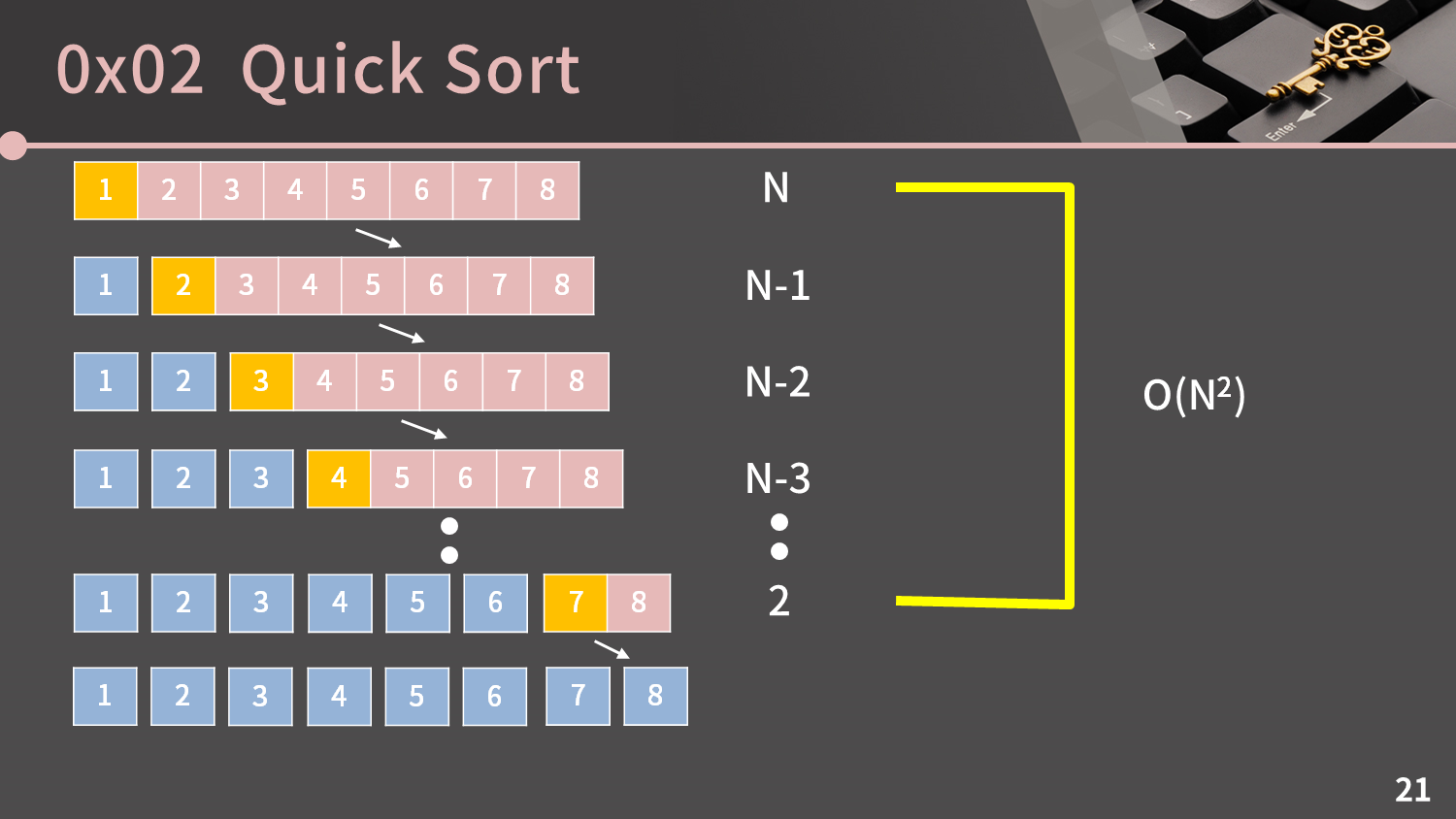
그런데 퀵 소트에는 아주 치명적인 단점이 있습니다. 1, 2, 3, 4, 5, 6, 7, 8을 퀵 소트로 정렬하면 시간복잡도가 얼마일지 생각해봅시다. 안타깝게도 매번 선택되는 pivot은 중앙에 가는 대신 제일 왼쪽에 위치하게 되고 그로 인해 단계는 lg N개가 아닌 N개가 됩니다. 그리고 시간복잡도를 계산하면 O(N2)입니다. 이 경우에서 볼 수 있듯이 퀵 소트는 평균적으로 O(NlgN)이지만 최악의 경우 O(N2)입니다. 그리고 단순히 제일 왼쪽의 값을 pivot으로 선택해보면 지금처럼 리스트가 오름차순이거나 내림차순일 때에 바로 O(N2)이 됩니다.

STL이 없을 때 정렬을 직접 짜야 한다면 퀵 소트를 절대 쓰지 마라고 맨 처음에 계속 말한 것도 이 이유 때문인데 머지 소트가 퀵 소트보다 느린건 맞지만 어차피 O(NlgN)에 돌아가니 충분히 빠릅니다. 그러면 최악의 경우 O(N2)인 퀵 소트를 절대 쓸 필요가 없습니다. 다시 한 번 말하지만 직접 정렬을 짜야할 때 퀵 소트를 쓰면 안됩니다.